Boolean Algebra and Logic Gates

Brief Intro

What are logic gates and why are they useful? A long time ago a man named Bool introduced boolean algebra which is the core foundation of digital logic! You might ask how is that even useful? Bear with me for a minute because this kind of mathematics are super important and kinda fun!

Boolean algebra has some variables that are pretty simple. They can only be in two (2) states either zero (0) or one (1), as in False or True. By taking one or more variables we can do logical operations with them and there are quite a lot of them. One of the most simple operators are AND, OR and NOT so let's dive right into those three.

NOT Operator - Negation

The NOT operator is very easy. It takes a a variable and just negates it. So for example if we have a variable of zero as in False, if we negate it the output will be one as in True. In order to represent all of the operations and possible outcomes we can use the so called truth tables to concisely represent everything. Here is a truth table of the NOT operator.

The notation used for negation is signified with "¬".

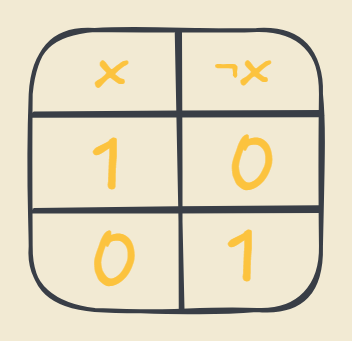
Note that if we negate something twice nothing really changes since we get back where we started from so ¬¬ X is equivalent to X and is written as ¬¬ X ≡ X. The tribar is often seen in mathematics where there is an equivalence of two different things.

OR Operator - Disjunction

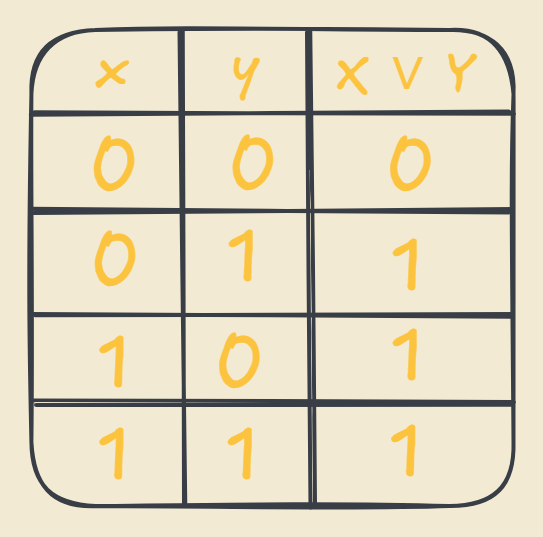
The OR operator which is also referred as a disjunction is annotated as X ∨ Y and outputs True if one of the inputs are True.

AND Operator - Conjunction

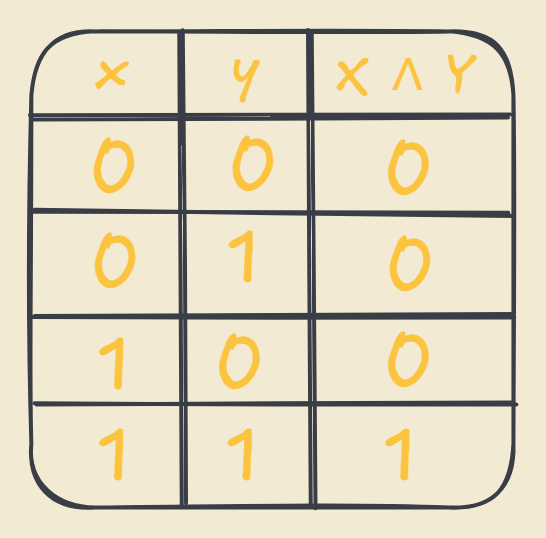
The AND operator which is a conjuction is annotated as X ^ Y. AND outputs True only if both of the input X and Y are True.

Exclusive OR (XOR)

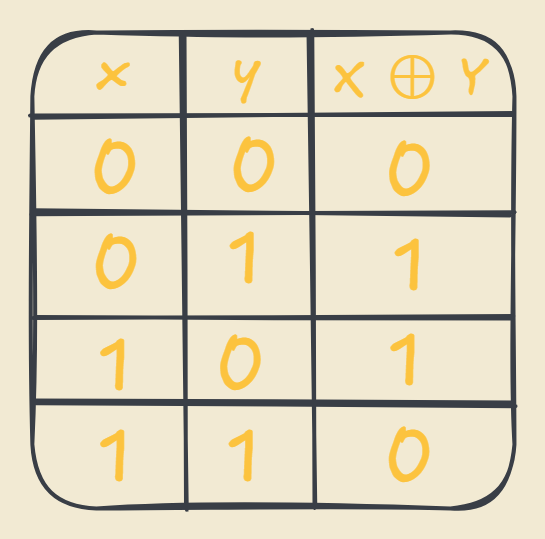
The operation of XOR that is referred as exclusive is annotated with a circle and a cross in the middle as such X ⊕ Y. XOR outputs True only if one of the inputs is True. It is similar to the OR operator but in this case when both of the inputs are True then the XOR operator outputs false hence the exclusive.

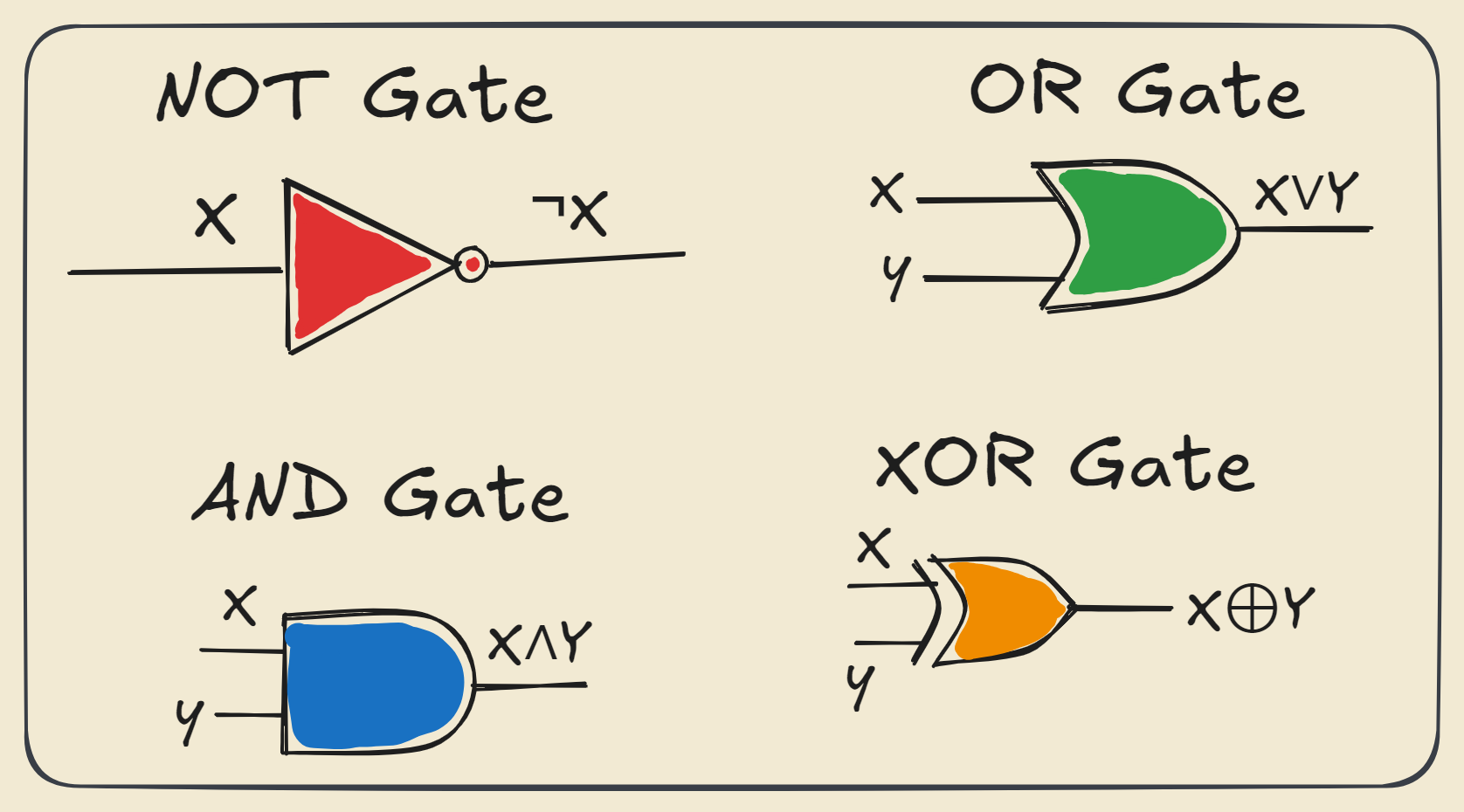
Logic Gates

Logic gates are devices that peform the logical operations we previously saw. They take one or more binary inputs and produce an output. They can be found nearly everywhere as they are the foundation of digital devices. Here are the previous logical operations drawn with logic gates.